Solstice drift, and how to fix it
January 12th, 2013 at 11:54 pm (Astronomy, Planets, Society)
 The summer and winter solstices happen around the 20th of June and December, respectively. Around the 20th? That seems rather… imprecise, for an astronomical event with a precise definition: the time at which the Sun reaches its “highest or lowest excursion relative to the celestial equator on the celestial sphere” or, for the viewer standing on the Earth, its highest or lowest altitude from the horizon. This is determined by the Earth’s orbit and corresponds to the time at which your current hemisphere’s pole points most closely to, or farthest from, the Sun. So why doesn’t it happen at the same time each year?
The summer and winter solstices happen around the 20th of June and December, respectively. Around the 20th? That seems rather… imprecise, for an astronomical event with a precise definition: the time at which the Sun reaches its “highest or lowest excursion relative to the celestial equator on the celestial sphere” or, for the viewer standing on the Earth, its highest or lowest altitude from the horizon. This is determined by the Earth’s orbit and corresponds to the time at which your current hemisphere’s pole points most closely to, or farthest from, the Sun. So why doesn’t it happen at the same time each year?
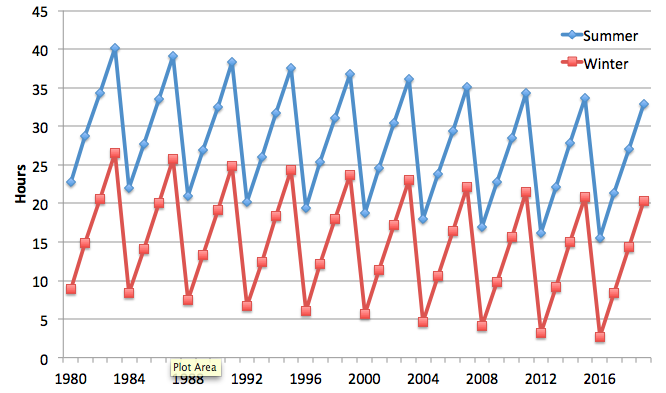
Inspired by an awesome book I recently acquired (“Engaging in Astronomical Inquiry” by Slater, Slater, and Lyons), I decided to investigate. I used the Heavens Above site to pull up historical data for the summer and winter solstices going back to 1980. I plotted the time for each solstice (in Pacific time) as its offset from some nearby day (June 20 or December 21). And sure enough, here’s what you get:
The solstice time gets later by about 6 hours each year, until a leap year, when it resets back by 24 – 6 = 18 hours.
Of course, the solstice isn’t really changing. The apparent change is caused by the mismatch between our calendar, which is counted in days (rotations of the Earth), and our orbit, which is counted in revolutions around the Sun. If each rotation took 1/365th of a revolution, we’d be fine, and no leap years would be needed. But since we’re actually about 6 hours short, every 4 years we need to catch up by a full rotation (day).
Now, we all know about leap years and leap days. But this is the first time I’ve seen it exhibited in this way.
Further, you can also see a gradual downward trend, which is due to the fact that it isn’t *exactly* 6 hours off each year. It’s a little less than that: 5 hours, 48 minutes, and 46 seconds. So a full day’s correction every four years is a little too much. That’s why, typically, every 100 years we fail to add a leap day (e.g., 1700, 1800, 1900). 11.25 minutes per year * 100 years = 1125 minutes, and there are 1440 minutes in a day. But that’s not a perfect match either… which is why every 400 years, we DO have a leap day anyway, as we did in the year 2000.
This is what, in computer science, we call a hack.
And now it is evident why for every other planet, we measure local planet time in terms of solar longitude (or Ls). This is the fraction of the planet’s orbit around the Sun, and it varies from 0o to 360o. It’s not dependent on how quickly the planet rotates. It’s still useful to know how long a planet’s day is, but this way you don’t have to go through awkward gyrations if the year is not an integral multiple of the day.
By the way, you can get a free PDF version of ‘Engaging in Astronomical Inquiry’. If you try it out, I’d love to hear what you think!
Vali said,
January 13, 2013 at 2:01 am
This is really interesting, Kiri, and you are so good in explaining how it works. Thanks! I learned something new today. :)
Susan said,
January 14, 2013 at 3:36 pm
Hello! Your blog dropped off my reading list by accident, but I’m back now :).
Jon said,
January 30, 2013 at 11:23 pm
I did not know this!