What I Learned Today

Adventure 2 in “Adventures with a Microscope” is titled “We Become Crystal Gazers.” The author continues:

We are not going to peer into such crystals as fortune tellers use, in which they claim to be able to predict that some rich relative is going to leave you money, or some equally nonsensical bosh.

No indeed, this is about chemistry. So I followed along, heated some water, and mixed up supersaturated solutions of various interesting substances from my kitchen. And wow, check it out! (Click to enlarge.)

Salt. Best viewed ~1 hour after deposition on the slide, with partial crystal formation; if you wait longer, the slide becomes crowded, and since the crystals are cubes, it’s hard to get them all in focus (too much relief!). I love this shot. It reminds me of Flatland.

More salt, the next day, with larger crystals.

Baking soda, which apparently creates sparry crystals.

Sugar! This one took a full day to form interesting crystals. But wow, they are gorgeous!

More sugar, almost a butterfly-like configuration. I expect the symmetry is coincidence.

The biggest surprise for me — my saliva, 24 hours later, had created these awesome fractal patterns. At first I thought it might be nucleation following tiny scratches in the slide glass, but the fact that they’re fractal renders this unlikely. No clue what this is, but my best guess is that it’s just random diffusion patterns, like these manganese fractal patterns.

Aha, I found an article titled “Dendritic growth in viscous solutions containing organic molecules” which has these great examples:


Caption: “Crystal patterns of some body fluids: (a) saliva; (b) cerebrospinal fluid; (c) urine; (d) blood serum.”

My examples seem to match the “blood serum” image the best, but I assure you it was saliva. Not sure what’s going on in their sample (a)!

The more I panned across the expanse of fractal growth, the more it started looking like a map of a European city. Is it not marvelous?

I think I’ve finally figured out the longtime mystery about why tea both wakes me up and calms me down (anxiety-wise). I consistently feel a physical effect after drinking a cup of tea, as if a knot inside my stomach dissolves, and problems don’t seem quite as pressing, and it’s easier to be friendly and sociable. This sounds like the opposite of caffeine, which is known to increase irritability.

But just recently, I stumbled on a possible explanation. It’s not the caffeine at all! It’s something called L-theanine:

“Theanine is able to cross the blood-brain barrier and appears to have psychoactive properties. […] it appears to increase levels of the inhibitory neurotransmitter GABA, and to a lesser degree, dopamine.”
Source: livestrong.com

L-theanine is often mentioned in conjunction with green tea, but it is also found in black tea. This article says green tea has about 8 mg per cup, while therapeutic doses of the stuff (for anxiety disorders) are more like 200-600 mg. Another source indicates 15-30 mg per cup, and that “L-theanine increases the production of dopamine and serotonin, two brain chemicals associated with alertness, pleasure, and a good mood.”

Further, there’s evidence of a lack of side effects (at least in rats):

“In 2006, a study conducted on rats administered super-high doses of L-theanine daily for a 13 weeks found no consistent or significant negative effects on behavior, food intake, body weight, clinical chemistry, urine, blood, morbidity or mortality.”
Source: livestrong.com

Therefore, I should be free to experiment away. And if theanine is the active agent, then I should get the same mood benefits (though not the wake-me-up effect) from decaf green tea. If only it were easier to do controlled experiments on oneself!

As you may have learned in high school chemistry, a mole is 6.022 x 10²³ of something (usually something really tiny, like atoms). This seemingly arbitrary value is also known as Avogadro’s number. Why is it named after him, and how did that value come to be chosen?

Avogradro’s full name was Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e di Cerret, and he had nothing to do with defining the value for a mole. Instead, he came up with the ideal gas law, which says that two samples of gas that occupy the same volume (with the same temperature and pressure) also contain the same number of molecules. It is most often encountered as pV = nRT. In 1909, 53 years after Avogadro died, Jean Perrin proposed naming the value of a mole after him.

Beyond Avogadro, why use 6.022 x 10²³ as the basis for a mole? The history of this decision is an interesting illustration of what happens when a common value must be chosen for convenience, but there is no physical reason to prefer one over another (a similar situation arises for planetary coordinates; latitude has a well defined start point due to the axis of rotation, but longitude has to be given a start point arbitrarily). Originally, and quite logically, chemists used hydrogen (the simplest element, with only one proton) as a basis for computing atomic weights. They set H=1 and computed values for everything else relative to hydrogen. Later others proposed using oxygen as a standard (O=16), since oxygen is so prevalent and combines with so many things, and after decades of debate, in 1961 they finally settled on using carbon (C=12) as the standard. And so the value for a mole was born: the number of atoms in 12 grams of carbon-12 (isotopes matter!). (How do you count them though? See here.)

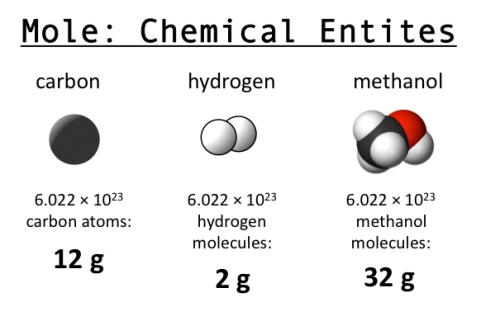Why do we care? The mole is useful because of stoichiometry, one of my favorite words ever. If you know that you need 2 hydrogen atoms for every 1 oxygen atom to make water, then you know you need 2 moles of H for every 1 mole of O. A 2:1 ratio based on weight or volume won’t work, but you can convert moles into grams with knowledge about the atomic weight of each. This tells you exactly how much to mix to get the result you want, without wasting anything. Very efficient! (Image from Clear Science.)

Even though it came from just 12 grams of carbon, a mole is a really, really big number. No, really. I love these analogies (from CDLI’s Chemistry 2202 course) that help us understand how big:

How big is a mole?

• one mole of peas is enough to cover Earth and 250 more planets the same size as Earth one metre deep in green peas
• a stack of one mole of pennies is tall enough to reach Proxima Centauri (the second closest star to Earth) and back again 7448 times
• a mole of marbles spread over the Earth would cover it to a depth of 80 km
• if you own a mole of dollars and you spend a billion dollars a day, then you could spend that amount per day for over a trillion years before you run out of money. (Earth has only been around for 4.5 billion years i.e. that’s 0.45% of a trillion years!)

For more molar fun, I highly recommend this mole lesson/activity. And six months from now, you can celebrate Mole Day: October 23, from 6:02 a.m. to 6:02 p.m.

It happened so long ago that it’s not really known how glass was first discovered. Certainly, lightning can strike a sandy beach and fuse silicon into glass bits (called fulgurites). The lightning has to reach 3270 F for this to happen, which would be difficult for ancient human cultures to reproduce, although there are tales of sailors inadvertently using sodium carbonate blocks around a fire ring on the beach, which reduces the melting point of glass to 2552 F, more likely to be within reach. According to wikipedia, a candle flame reaches about 1800 F, and a blowtorch gets up to 2370 F, and a Bunsen burner can get up to 2900 F — so chemistry lab students out there should be able to get right to work on glass-making!

Interestingly, glass made with sodium carbonate (also called niter) isn’t very stable; it gradually dissolves from contact with water (which makes terrible windows or water glasses). More stable glass can be made by adding calcium carbonate (lime), which is what is still done today. Other additives create color tints and other properties. Here are some glass recipes with suggested proportions. The wikipedia article on glass is full of other fascinating tidbits.

And yes, glass is generally considered to be a solid (albeit an amorphous one, meaning it has no crystalline structure) rather than a liquid.

If you had to pick reference points to define a new temperature scale, what would you use? If you were Daniel Gabriel Fahrenheit, a glassblower and chemist, you picked: the equilibrium temperature of a specific brine, the temperature at which water freezes, and the temperature of the human armpit. Apparently, he used his wife as his calibration reference. The brine is interesting: a frigorific mixture of ice, water, and ammonium chloride. Frigorific indicates that the mixture goes to an equilibrium temperature no matter what the initial temperatures of the components were. Water + ice is a frigorific mixture that goes to 32 F (or 0 C).

Next, what numbers do you assign to these reference points? Fahrenheit assigned 0 F to the brine, 32 F to the ice, and 96 F to human body temperature. The seemingly arbitrary numbers arose because Fahrenheit modeled his system after the Romer scale, which assigned 0 degrees to brine and 60 degrees to boiling water, which put the freezing point of water at an awkward 7.5 degrees. Fahrenheit multiplied everything by 4, got 96 degrees for the human body, and then fudged his definition of a degree (which just means a “step”) a bit so that the freezing point of water would be exactly 64 degrees less than body temperature (so, 32 F). Why? So that his thermometers could be easily marked between those two points — 64 is a power of 2 and that means it’s easy to get equal divisions by repeatedly marking the midpoint between existing marks.

Fahrenheit published his scale in 1724. Later, the scale was revised so that there would be exactly 180 degrees between the freezing and boiling points of water (180 being a number that is divisible by a conveniently large number of numbers). This pushed the human body temperature up, on the Fahrenheit scale, to 98.6 F.

That’s all very interesting, but you have to wonder: once you’ve invented a new scale, how do you persuade others to use it? I’m wondering what kind of marketing Fahrenheit employed, other than his presentation at the Royal Society of London. Clearly, it was quite effective… until Anders Celsius came along 20 years later.