CS 461 Homework 4
Due: Midnight, February 26, 2009
Please your answers to these questions in <yourlastname>-hw4.txt (or
PDF).
Part 1: Parametric Methods (45 points)
For what kinds of situations is the Bernoulli distribution a good choice as a parametric model? Give an example. (5 points)
If I flip a coin and get { tails, heads, tails, tails, tails, heads, heads }, what is the maximum likelihood estimate of the probability of getting heads? (5 points)
Imagine that I always assume ("estimate") that the probability of getting heads from any coin is 0.5 (i.e., I assume that they are all fair coins). If I find a coin that is off-balance, so that P(heads) for this coin is really 0.57, what is the bias of my estimate for this coin? (5 points)
How is the MAP estimate different from the maximum likelihood estimate of a given value theta? (5 points)
Weka: This time, you'll get a chance to use Weka's "Experimenter", which makes it easy to compare several classifiers on the same data set(s). You may want to use the same technique for part of your project!
The data set you will use is wine.arff. It contains three classes, each of which corresponds to wine from a different cultivar (1, 2, or 3). There are 13 features, which are the results of different chemical analyses of the wine. Human wine tasters often claim to be able to distinguish among these three types -- let's see if machine learning can also learn to do it.
First, what is a baseline you might use to evaluate any machine learning algorithm against, on this problem? Remember, a baseline should assign a new wine sample to one of the three classes, without observing any of the features. (5 points)
Now, to get started, run Weka and click on "Experimenter" (instead of "Explorer"). The "Setup" panel should appear. Click "New" to create a new experiment. Leave all of the defaults set (Experiment type-> Cross-validation, 10 folds, Classification).
Under "Datasets", click "Add new..." and browse to add this file: wine.arff. We'll just use one data set, but in general you could add more to see how your algorithm does on many different problems.
Under "Algorithms", click "Add new.." and click "Choose" to pull up the same algorithm chooser that we used before. Add each of the following, clicking "OK" after each one:
- k-NN: lazy -> IBk, then set "KNN" to 3 to specify the use of the three nearest neighbors.
- DT: trees -> J48, leave "unpruned" set to "False" (so it prunes).
- SVM: functions -> SMO, then set "kernel" to "RBFKernel" (Gaussian kernel) and set "gamma" to 0.1.
- ANN: functions -> MultilayerPerceptron, set "hiddenLayers" to 3 (indicates a single hidden layer with 3 nodes).
- Naive Bayes: bayes -> NaiveBayes, use the defaults.
Now switch to the "Run" panel and click "Start". This will do 10 runs of 10-fold cross-validation (splitting the folds differently each time). It may take a while!
Report your results: (5 points) Switch to the "Analyse" panel and click "Experiment". To compare the accuracy achieved by each method, leave all of the settings on their defaults and click "Perform test". This will report the average accuracy achieved by each algorithm. List the results you got, one number (accuracy) for each of the five algorithms.
Which algorithm performed the best?
Analyze your results: (15 points)
Set "Comparison field" to "UserCPU_Time_training" and click "Perform test".
List all of the results (ignore the "v"s). Which one took the longest to train?Set "Comparison field" to "UserCPU_Time_testing" and click "Perform test". List all of the results. Which one took the longest to test?
Part 2: Clustering (55 points)
When using the k-means clustering algorithm, we seek to minimize the variance of the solution. In general, what happens to the variance of a partition as you increase the value of k, the number of clusters, and why? (5 points)
For what value of k can you always get a variance of 0? Why? (5 points)
Show 2 iterations of the k-means algorithm (k=2) on the following one-dimensional data set: (10 points)
Data: [ 4, 1, 9, 12, 6, 10, 2, 3, 9 ]
First iteration: cluster centers (randomly chosen): 1, 6
Data assignment:
- Cluster 1: { 1, 2, 3 }
- Cluster 2: { 4, 9, 12, 6, 10, 9 }
Show the cluster centers, then the data assignments, that would be obtained for each of two more iterations.
After your iterations, has the algorithm converged to a solution at this point, or not? How can you tell?
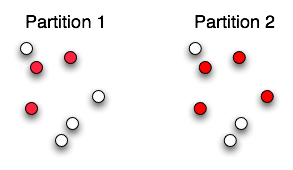
Consider the following diagram showing the same 7 balls that have been clustered into two different partitions. In each partition, there are two clusters (red and white). Cluster membership of an item is indicated by the item's color. What is the Rand Index of agreement between the two partitions? Show your work. (10 points)
Weka: Go back to the "Explorer" to do some clustering. Load in segment2.arff. This data set contains four different kinds of 3x3 pixel image regions (sky, window, grass, cement). Select the "Cluster" tab. Click "Choose" and select SimpleKMeans. Click on its name to change "numClusters" to 4. Set "seed" to 0. Under "Cluster mode", select "Classes to clusters evaluation" and make sure "(Nom) class" is specified below that. Click "Start".
Weka will show you the mean of each cluster (across all features) and then show a confusion matrix that compares the clusters you got with the "true" class labels in the data. Since k-means doesn't know which class is which, they may not line up in the order you expect. Below the confusion matrix, Weka tells you which class is the most likely match for each cluster. It then reports the number of incorrectly classified instances.
Show the confusion matrix you obtained, with the rows re-arranged so that the "correctly clustered" items are on the diagonal. That is, the first row should be the class that matches cluster 0, the second row should be the class that matches cluster 1, etc. (5 points)
How many items were incorrectly clustered? (5 points)
What are the mean values for the "rawred", "rawblue", and "rawgreen" features for the cluster associated the "grass" class? (2 points)
Now do the same thing with EM. Click "Choose", select "EM", and then specify that "numClusters" should be 4 and "seed" should be 0. Now the output is not just a mean for each feature, but instead includes a standard deviation.
Show the re-arranged confusion matrix for EM: (5 points)
How many items were incorrectly clustered? (5 points)
What are the mean and standard deviation values for the "rawred", "rawblue", and "rawgreen" features for the cluster associated the "grass" class? (3 points)
What to turn in
Upload this file to CSNS under "Homework 4":
<yourlastname>-hw4.txt(or<yourlastname>-hw4.pdfif you prefer to submit in PDF format)
Extra credit
If you wish to tackle some extra credit, you may do so here. You can earn up to 5 points to be applied to any of your homework assignments (but not to exceed 100 on any assignment). To receive these points, you must get at least a 70% on the main part of Homework 4, so finish the regular assignment before moving on to this part.
- A recent development in the world of clustering has been the
ability to incorporate prior knowledge when clustering.
This paper shows how to incorporate knowledge about individual pairs of data points, in terms of whether they should or should not be clustered together. Explain, in your own words, how this is accomplished. (5 points)
What to turn in
Upload this file to CSNS under "Homework 4: Extra Credit":
<yourlastname>-hw4-extra.txt(or<yourlastname>-hw4-extra.pdfif you prefer to submit in PDF format)